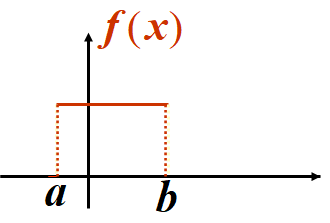概率论-随机变量与概率分布
Wirten by ZLH ©️
2.1 随机变量
随机变量的定义
▶️ 设 E 是随机试验,它的样本空间是 S={e} 如果对于 每一个 e∈S, 有一个实数 X(e) 与之对应,这样就得到 个定义在 S 上的单值实值函数 X(e)。称 X(e) 为随机变量。
随机变量常用 X,Y,Z 等表示,对应取值相应的用 x,y,z 等表示。
👀注意 : 随机变量是定义在样本空间的实值集函数,它与普通的实函数有本质的区别。一方面它的取值是随机的,另一方面它取每一值都有一定的概率。
随机变量分类
2.2 离散型随机变量的概率分布
离散型随机变量概率分布的定义
▶️设离散型随机变量 X 所有可能取的值为 xk(k=1,2,⋯),X 取 各个可能值的概率,即事件 {X=xk} 的概率 ,为
P{X=xk}=pk,k=1,2,⋯
称此为离散型随机变量 X的分布律,也称概率分布。
$ p_{k}$的性质
- 非负性 : pk≥0,k=1,2,⋯;
- 规范性 : ∑k=1∞pk=1∘
👀所有的离散型随机变量分布律都要满足上述性质,否则这个分布律就是错的。
常见问题
利用已知离散型随机变量的分布律求该随机变量对应的样本空间内某些随机事件的概率。
常见离散型随机变量分布
介绍五种常见的随机变量分布情况
1、0-1分布
▶️如果随机变量X只能取 0,1 两个值, 其分布律为
P(X=1)=p,P(X=0)=1−p(0<p<1)
或 P(X=k)=pk(1−p)1−k,k=0,1
则称 X 服从参数为 p 的 (0−1) 分布或两点分布,记为 X∼B(1,p).
2、二项分布
▶️在 n 重贝努里试验中, 若设 P(A)=p,P(Aˉ)=1−p,则 事件 A 恰好出现 k(0≤k≤n) 次的概率是
P(X=k)=Cnkpk(1−p)n−k(k=0,1,⋯n)
则称 X 服从参数为 n,p 的 分布二项,记为 X∼B(n,p).
特别的,n=1是两点分布。
(0-1)分布是1重贝努利试验,将n个1贝努利实验的结果相加,则是二项分布的场景。
二项分布的性质
-
性质1:设 X∼B(n,p), 则当 k=[(n+1)p] 时, P(X=k) 取得最大值.
👀该性质可以通过单调性来证明。
👀该性质表示二项分布的概率分布呈现“峰”状,存在一个概率最大值对应的k
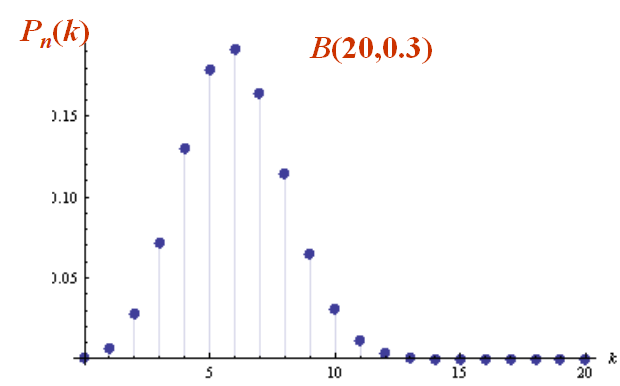
-
性质2:泊松定理
若 X∼B(n,p), 则当n比较大而 p 又很小时,有以下泊松近似计算公式
P(X=k)=Cnkpk(1−p)n−k≈k!λke−λ,k=0,1,⋯,n
其中 λ=np.
👀n越大,p越小,λ=np大小适中的情况下,近似解更精准。一般来讲,n≥100,np≤10近似效果较好。
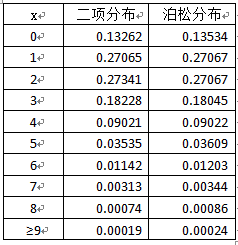
3、泊松分布
▶️若随机变量 X 的所有可能取值为一切非负整数,且它的分布律为
P(X=k)=k!λke−λ,k=0,1,2,⋯
其中 λ>0 ,则称 X 服从参数为 λ 的泊松分布(Poisson distribution ),记为 X∼π(λ)
泊松分布的分布律满足:
(1) P(X=k)=k!λke−λ⩾0,k=0,1,2,⋯ (2) ∑k=0∞P(X=k)=∑k=0∞k!λke−λ=e−λ∑k=0∞k!λk=e−λ⋅eλ=1
👀泊松分布是概率论中最重要的概率分布之一。泊松分布的本质还是二项分布,泊松分布是用来简化二项分布计算的,并可以用来计算一些稀有随机事件发生的概率。
👀泊松分布是以 n,pn 为 参数的二项分布当 n→∞ 时 (limn→∞npn=λ) 的极限分布,当 n 很大, pn 很小时,可用泊松分布进行二项分布的近似计算(泊松定理)
👀性质:设 X∼π(λ), 则当 k=[λ] 时, P(X=k) 取得最大值. 【这和二项分布类似】
判断泊松分布
考察一个变量是否服从泊松分布,需要满足以下条件:
- X是在一个区间(时间、空间、长度、面积、部件、整机等等)内发生特定事件的次数,可以取值为0,1,2,…;
- 一个事件的发生不影响其它事件的发生,即事件独立发生;
- 事件的发生率是相同的,不能有些区间内发生率高一些而另一些区间低一些;
- 两个事件不能在同一个时刻发生;
- 一个区间内一个事件发生的概率与区间的大小成比例。
满足以上条件,则X就是泊松随机变量,其分布就是泊松分布。
❓例题:
假设我们有一批零件,它的次品率是0.1%,也就是千分之一。请问我们生产一千个产品当中至少有两件次品的概率?
📺【分析】:很容易从反面理解题意是要求解没有次品和只有一次次品的概率,这也是符合二项分布的。但是如果使用二项分布公式来解答,就要求解0.999的1000次方,这很麻烦。又因为$\lambda=np $满足当 n 很大, p 很小时,可以用泊松分布来近似计算。
📖【解答】:
λ=np=1000∗0.001=1P(k≥2)=1−P(k=1)−P(k=0)=1−1!11e−1−0!10e−1≈0.264
❓例题2:

4、超几何分布
▶️在 N 件产品中有M 件不合格品,从中任取 n 件检查,(n≤M), 记X为取到的次品数,则
P(X=k)=CNnCMkCN−Mn−k,k=0,1,…,n
称随机变量 X 服从参数为n, N,M 的超几何分布,记作
X∼H(n,M,N)
👀注意:这种抽样相当于不放回抽样。
如果是可以放回的抽样,则场景相当于是p=NM的一个二项分布, X∼B(n,p).
👀当N很大的时候,超几何分布可以用二项分布来近似。
N→∞limCNnCMkCN−Mn−k=Cnkpk(1−p)n−k,k=0,1,2,⋯,min(M,n)
5、几何分布
▶️设随机变量 X 的所有可能取值为1, 2,3,⋯, 且
P(X=k)=(1−p)k−1p,k=1,2,3,⋯
其中 0<p<1,则称 X 服从参数为p的几何分布, 记作 X∼G(p)
几何分布的分布律满足:
(1) P(X=k)≥0 (2) k=1∑∞P(X=k)=1
几何分布性质
几何分布具有无记忆性,即
P(X>m+n∣X>m)=P(X>n)
❓例题:
某人向一目标进行射击,直到击中目标为止,已知每次击中的概率为0.3,试求射击次数不超过3的概率。
📺【分析】:
判断几何分布的情况,分布条件是前k-1次都是失败,最后一次成功,这种分布和0-1分布有点类似,但是有了**“顺序性”**
📖【解答】:
设射击次数为X, 则X∼G(3)
P(X≤3)=P(X=1)+P(X=2)+P(X=3)=0.3+(1−0.3)×0.3+(1−0.3)2×0.3=0.657.
2.3随机变量的分布函数
分布函数的引入解决了分布律并不够表示非离散型随机变量以及我们常常需要计算区间概率的一些场景,是基于随机变量分布律的一个函数。
分布函数的定义
▶️设 X 是一个随机变量,称
F(x)=P(X≤x)(−∞<x<+∞)
为 X 的分布函数, 记作 F(x).
如果将 X 看作数轴上随机点的坐标,那么分布函数 F(x) 的值就表示 X 落在区间 (−∞,x] 内的 概率。
👀注意:
-
(1) 在分布函数的定义中, X 是随机变量, x 是参变量.
-
(2) F(x) 是随机变量 X 取值不大于 x 的概率.
-
(3) 对任意实数 x1<x2 ,随机点落在区间 (x1,x2] 内 的概率为:
P{x1<X≤x2}=P{X≤x2}−P{X≤x1}=F(x2)−F(x1)
因此,分布函数完整地描述了随机变量的统计规律性。
-
(4) 需要在实际问题中区分好端点情况,尤其是对于离散型随机变量来说,有时候需要对端点处随机变量值单独判断。
分布函数基本性质
-
(1)0≤F(x)≤1
-
(2) F(x) 在 (−∞,+∞) 上是一个不减函数,即对 ∀x1,x2∈(−∞,+∞) 且 x1<x2, 都有F(x1)≤F(x2)
-
(3) 极限处情况:
F(−∞)=x→−∞limF(x)=0F(+∞)=x→+∞limF(x)=1
-
(4)F(x) 处处右连续,即 limx→x0+F(x)=F(x0)
👀性质(1)(3)常用用来解带参数的分布函数参数值。
离散型随机变量的分布函数
▶️一般地,设离散型随机变量 X 的分布律是
P{X=xk}=pk,k=1,2,…,N
则其分布函数为 F(x)=P(X≤x)=∑xk≤xpk
=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧0,p1,p1+p2,⋯⋯p1+p2+⋯+pk,⋯⋯1,x<x1x1≤x<x2x2≤x<x3xk≤x<xk+1x≥xN
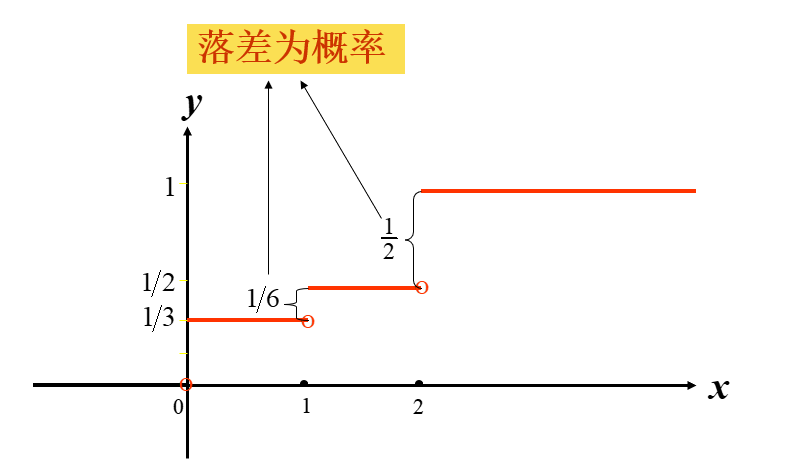

重要公式性质
- (1) P(a<X≤b)=F(b)−F(a)
- (2) P(X>a)=1−F(a)
通过(1)式引申得:
- P(a≤X≤b)=F(b)−F(a)+P(X=a)
- P(a≤X<b)=F(b)−F(a)+P(X=a)−P(X=b)
- P(a<X<b)=F(b)−F(a)−P(X=b)
连续型随机变量分布及概率密度
▶️对于随机变量 X, 如果存在非负可积函数 f(x) , x∈(−∞,+∞), 使得对任意实数 x, 有
F(x)=∫−∞xf(t)dt=P(X≤x)
则称 X为连续型随机变量, 称 f(x) 为 X 的概率密度函数,简称为概率密度。
将y=f(x)的曲线称作概率曲线。
👀这里的思想是:通过一个广义积分的转化,将分布函数转化成概率密度函数的积分,则分布函数可以直观地用曲边梯形面积来表示,区间的概率也可以用面积来表示。
从另外一个角度来说,比如0-1的数轴上无限小一点的概率,我们设为此处的概率密度是limx→x0P(x)=f(x),反过来,在一个区间内的概率就是对区间内概率密度函数求积分。
🌈参考资料:「概率论」三分钟告诉你抽象的概率密度是怎么来的
概率密度f(x)函数的性质
F(x)=∫−∞xf(t)dt
-
性质1:f(x)≥0, 且 ∫−∞+∞f(t)dt=1
因为 1=F(+∞)=∫−∞+∞f(t)dt
这个性质常用来求函数中的参数。
这条性质是——函数 f(x)是否为某一随机变量的概率密度的充要条件
-
性质2:对任意的实数 x1,x2(x1<x2)
P(x1<X≤x2)=∫x1x2f(t)dt
因为 原式=F(x2)−F(x1)=∫−∞x2f(t)dt−∫−∞x1f(t)dt=∫x1x2f(t)dt
由此性质,可得到: 对任意的实数 x0 有, P(X=x0)=0.
连续型随机变量取任意单点的概率为0,区别于离散型。
- 性质3:若 f(x) 在点 x 处连续,则有
F′(x)=f(x)
❓例题:
向某一目标发射炮弹,设弹着点到目标的距离(单位:米)X的概率密度为:
f(x)={12501xe−2500x2,0,x>0x≤0
如果弹着点到目标的距离小于50米时,即可以摧毁目标。现在向这一目标连发两枚炮弹,求目标被摧毁的概率。
📺【分析】:
弹着点到目标的距离有一个概率分布函数,首先根据概率密度函数求出概率,即每次发射炮弹目标被摧毁的概率,然后就是一个二项分布的问题了。
📖【解答】:
以Y 表示炮弹摧毁目标的次数。
P{X≤50}=∫−∞50f(x)dx=∫−∞00dx+∫05012501xe−2500x2dx=1−e1
则: Y∼B(2,1−e1).
P{1≤Y≤2}=1−P{Y=0}=1−C20(1−e1)0(e1)2=1−e21
三种重要的连续型随机变量
通过连续型随机变量的概率密度来给出三种常见的分布情况。
1、均匀分布
在概率论和统计学中,均匀分布也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。
▶️若随机变量X的概率密度为:
f(x)={b−a1,0,a<x<b 其它
则称 X在区间 (a,b) 上服从均匀分布,记作
X∼U(a,b)
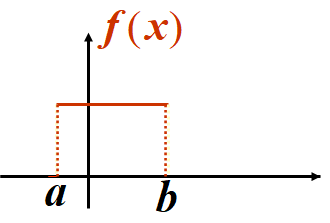
均匀分布的实质是等可能性,因此根据概率密度充要条件就可以推得其概率分布公式。
性质
若 X∼U(a,b),
1∘.对于长度为的区间 (c,c+l),a≤c<c+l≤b, 有
P{c<X≤c+l}=∫cc+lb−a1dx=b−al
2∘. X的分布函数为:
F(x)=P{X≤x}=⎩⎨⎧0,b−ax−a,1x<aa≤x<bx≥b
2、指数分布
指数分布是用来描述某个特定随机事件发生所需要等待的时间的分布的. 比如电子产品的寿命、顾客在某一服务系统接受服务的时间等.
▶️若随机变量X具有概率密度
f(x)={λe−λx,0,x>0 其它
其中 λ>0 为常数,则称 X 服从参数为 λ 的指数分布.
其分布函数为
F(x)=P{X≤x}={1−e−λx,0,x>0 其它
下图为f(x)的图像:
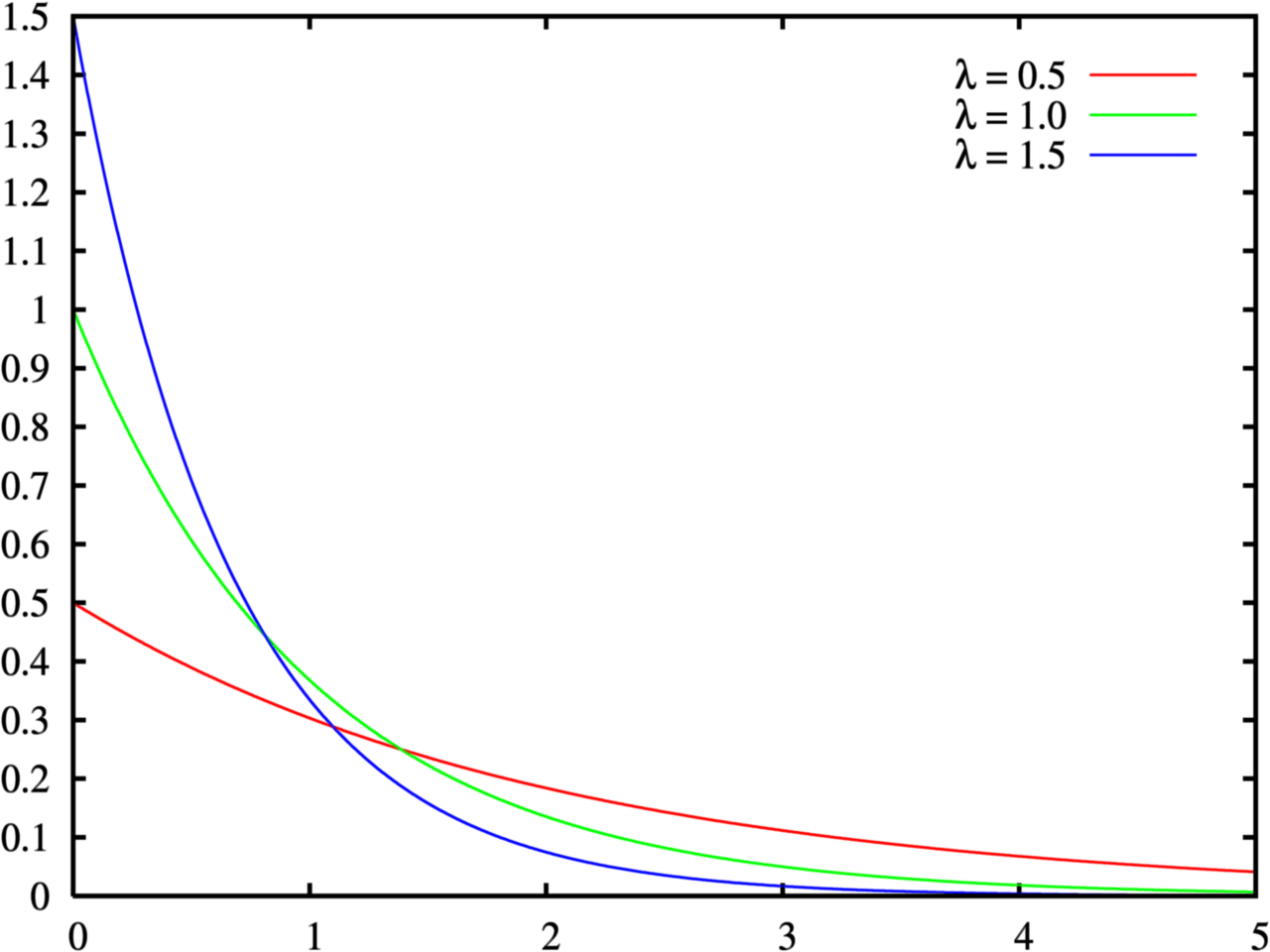
性质
- 无记忆性
指数函数的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,它的条件概率遵循:P(T>s+t∣T>t)=P(T>s) for all s,t≥0
理解指数分布我们要从伯努利分布 -> 二项分布 -> 泊松分布 -> 泊松过程 -> 指数分布的演变流程理解。
-
伯努利分布描述的是单次随机事件 (Pr=p) 的概率:
-
二项式分布预测的是多次(n次)独立随机事件 (Pr=p holds ) 发生的次数 (k 为自然数 )
Pr(K=k)=Cnk∗pk∗(1−p)n−k
-
泊松分布估计的是单位时间内随机事件的发生次数, 比如售后接到电话的概率。
事实上, 泊松分布是近似化连续化的二项分布, 当n很大, p 很小, n∗p 大小适合时,$\lambda $ =n∗p (用下自然数e的计 算公式就可以转化)。以接电话为例, 每个顾客打电话的概率都是p, 很小很小, 但是顾客数目很大 (n很大),我们就可以用 泊松分布来模拟 (k 为自然数 )
Pr(K=k)=k!λk∗e−λ
-
一维泊松过程就是t时间内的随机过程,有着和泊松分布中一样的$\lambda ,只是泊松分布观察的是单位时间,泊松过程中t改变,你把泊松分布中的\lambda 换成泊松过程中的\lambda * t$ 就是了(t是连续的,while K是离散的)
Pr(Xt0+t−Xt0=k)=k!(λ∗t)k∗e−λ∗t;
-
而指数分布描述的是泊松过程中,第k次随机事件与第k+1次随机事件出现的时间间隔。间隔大于t的概率就是 泊松过程中k=0的情况,(t是连续的)
Pr(T>t)=e−λ∗t
这是 只随时间变化的指数函数 !
如果X是一个等待时间,假设服从指数分布,那么 X>s+t 即等待时间超过s+t这个事件,以上公式意味着 给定我已经等待了t这么长时间,我再等s的概率与t没有关系,只跟s有关系。
说人话就是,举个例子,比如我在等公交车, 如果等公交车的时间服从指数分布,那么给定我已经 等了5分钟,我需要继续等,到第11分钟公交车还没来的概率, 与等6分钟公交车没有来的概率相 等: 未来我还需要等多长时间,跟我已经等了多长时间没有关系。
3、正态分布
▶️若连续型随机变量 X 的概率密度为
f(x)=2πσ1e−2σ2(x−μ)2,−∞<x<∞
其中 μ 和 σ(σ>0) 都是常数, 则称 X 服从参数为 μ 和σ2的正态分布或高斯分布. 记作
X∼N(μ,σ2)
称由 f(x) 确定的曲线为正态曲线。
正态分布曲线及其性质
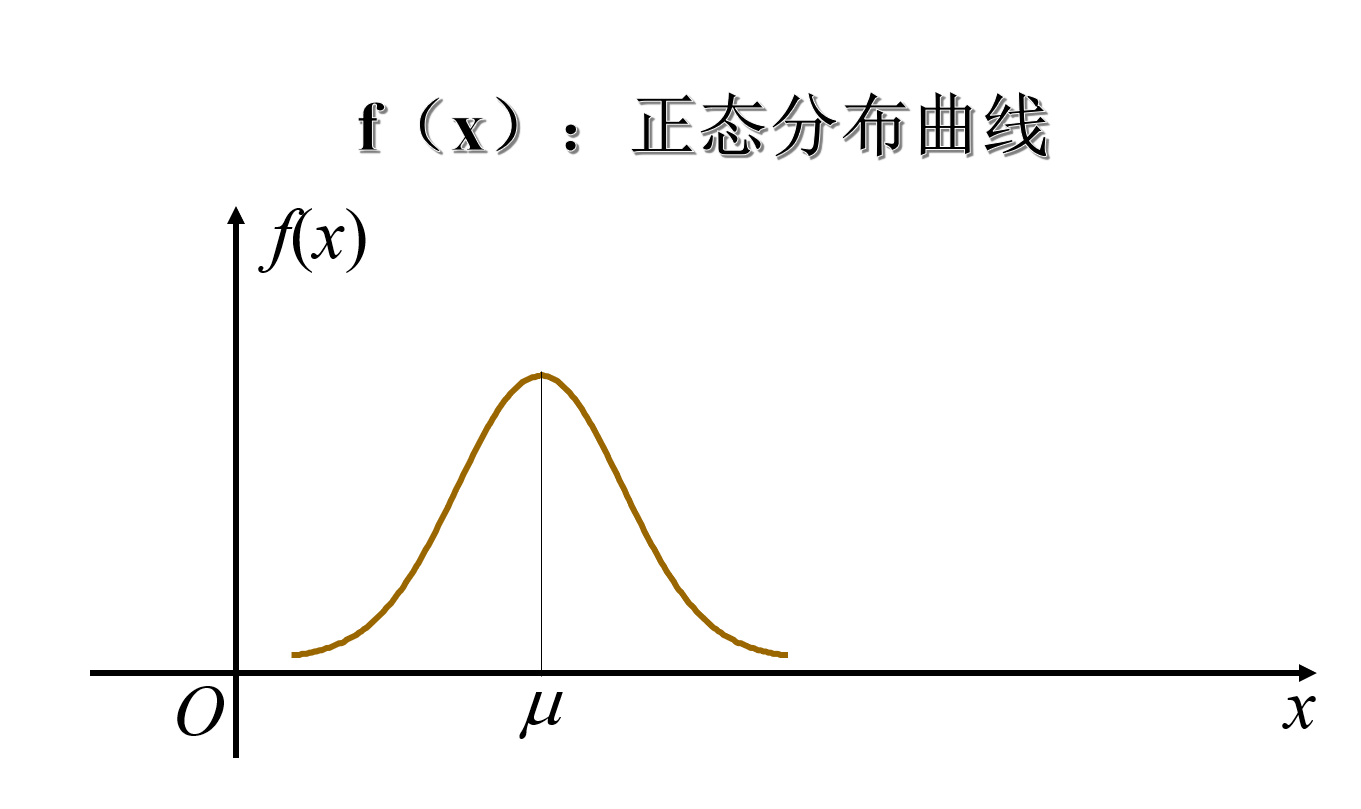
- 性质1: f(x)≥0
- 性质2: ∫−∞+∞f(x)dx=1
- 性质3:曲线 f(x) 关于 x=μ 对称;函数 f(x) 在 (−∞,μ] 上单调增加, 在 [μ,+∞) 上
单调减少, 在 x=μ 取得最大值;f(μ)=2πσ1
- 性质4:f(x) 以 x 轴为渐近线,当 x→∞ 时, f(x)→0.
- 性质5: x=μ±σ 为 f(x) 的两个抛点的横坐标;
在正态分布中的两个参数μ,σ有着重要的意义。μ是位置参数,改变对称轴的位置。σ是性状参数,决定了图形中峰的陡峭程度,σ越小,图形越高、越瘦;σ越大,图形越矮、越胖。
标准正态分布及其性质
▶️μ=0,σ=1 的正态分布称为标准正态分布.
其密度函数和分布函数常用 φ(x) 和 Φ(x) 表示:
φ(x)=2π1e−2x2,−∞<x<∞Φ(x)=2π1∫−∞xe−2t2dt,−∞<x<∞
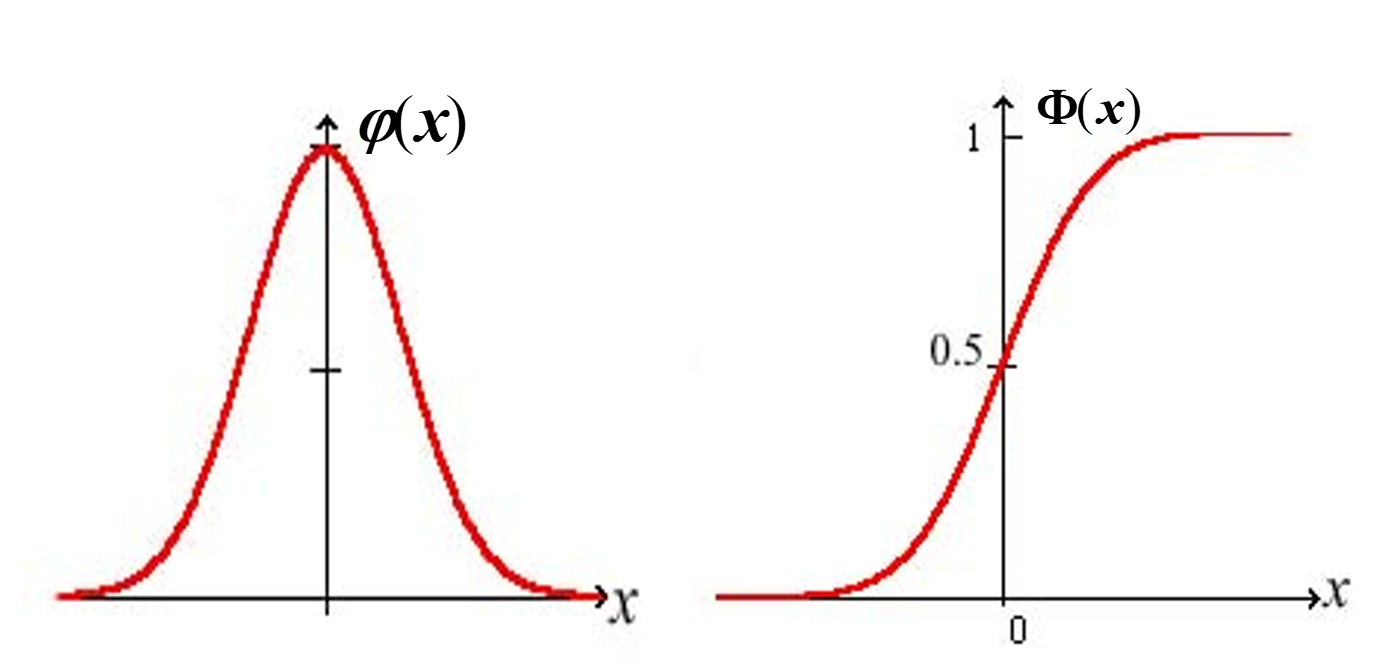
-
性质1:根据标准正态分布表
Φ(0)=21Φ(1.65)=0.9505≈0.95;Φ(2.33)=0.9901≈0.99;Φ(1.96)=0.975;Φ(2.58)=0.9951≈0.995
-
性质2:∀x∈R,Φ(−x)=1−Φ(x),或者写为Φ(−x)+Φ(x)=1
-
性质3:一般情况下,若X∼N(μ,σ2),只需要通过一个线性变换即可将一般正态分布化作标准正态分布:
定理 ▶️ 若 X∼N(μ,σ2), 则 Z=σX−μ∼N(0,1).
-
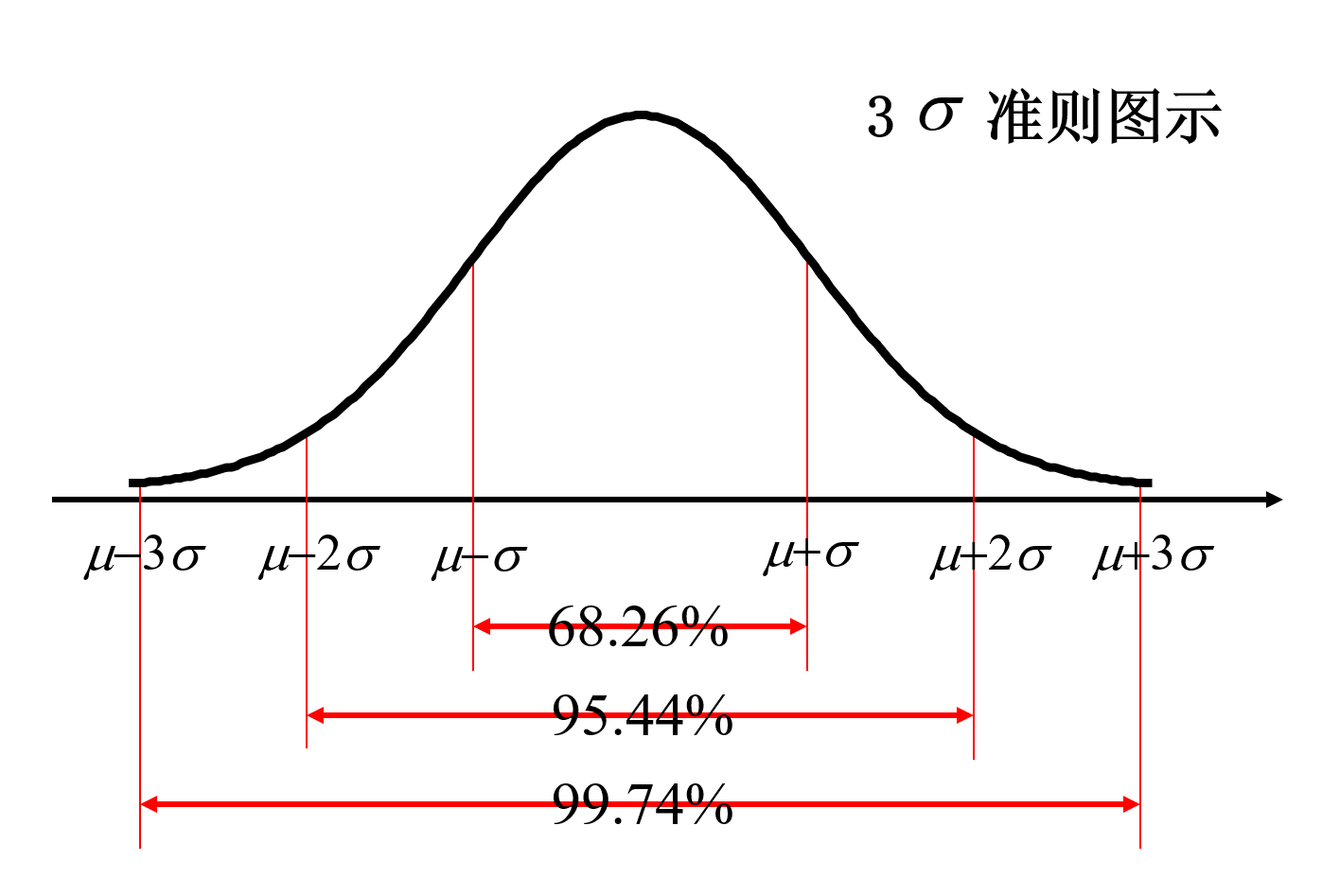
性质4:3σ 淮则:
X∼N(μ,σ2) 时,
P(∣X−μ∣≤σ)=Φ(1)−Φ(−1)=0.6826P(∣X−μ∣≤2σ)=Φ(2)−Φ(−2)=0.9544P(∣X−μ∣≤3σ)=Φ(3)−Φ(−3)=0.9974
可以认为, X 的取值几乎全部集中在
[μ−3σ,μ+3σ] 区间内.
这在统计学上称作 “ 3σ 准则” .
正态分布与标准正态分布的分布函数之间的关系
即通过对一般正态分布进行标准化来解决问题:
X∼N(μ,σ2)⇒FX(x)=P{X≤x}=P{σX−μ≤σx−μ}=Φ(σx−μ)P(a<X<b)=Φ(σb−μ)−Φ(σa−μ)
❓例题:
设 X∼N(2,σ2), 且 P{2<X<4}=0.3, 则 P{X<0}=________.
📺【分析】:
若进一步, P{X≥c}=P{X≤c}, 那么 c=2,也就是说,对称轴就是μ,左右两侧的概率分布各0.5
📖【解答】:
由对称性得 P{X<2}=0.5,P{0<X<2}=0.3,
所以 P{X<0}=P{X<2}−P{0<X<2}=0.5−0.3=0.2.
2.4一维随机变量函数的分布
离散型随机变量函数的分布
通过计算目标函数值分布的值做等价求得。
若出现“多对一”的映射情况,需要使用加法院里合并相同的随机变量,最后整理得到一张新的函数分布表。
连续型随机变量函数的分布
▶️:对连续性随机变量 X ,一般通过密度函数 fX(x) 或分布函数 FX(x) 来刻画其概率分布。
➡️如何求 Y=g(X) 的概率密度 fY(y) 呢?
一般步骤:
- (1) 先利用X的分布求出 Y 的分布函数 FY(y);
- (2) 利用 Y 的分布函数 FY(y) 求其概率密度 fY(y), 即fY(y)=FY′(y)
注意:
👀在求 P(Y≤y) 的过程中, 关键的一步是设法从 {g(X)≤y }中解出 X, 从而得到与{g(X)≤y} 等价的 X 的不等式.
例如,用 {X≤y−8} 代替 {Y=2X+8≤y}
用 {−y≤X≤y} 代替 {Y=X2≤y}
这样做是为了利用已知的X的分布,从而求出相应的概率。
这是求随机变量的函数的分布的一种常用方法.
定理:
▶️设随机变量 X 具有概率密度 fX(x),−∞<x<∞, 又 设函数 g(x) 处处可导且恒有 g′(x)>0( 或恒有 g′(x)<0), 则 Y=g(X) 是连续型随机变量, 其概率密度为
fY(y)={fX[h(y)]∣h′(y)∣,0,α<y<β, 其它
其中 α=min(g(−∞),g(∞)),
β=max(g(−∞),g(∞))
$ h(y)$ 是g (x) 的反函数.